A pair-of-pants is a surface that looks exactly like a pair-of-pants that you wear. Technically, it is topologically equivalent to a sphere which has been punctured three times, or a disk which had been punctured twice (shown below). It is an orientable surface of genus two having three boundary components. They are useful objects in topology, in that they give a different decomposition of surfaces. We usually think of closed connected surfaces as spheres, where either handles or cross-caps have been added. More formally, recall the Classification of Surfaces Theorem: Any closed, connected surface is topologically equivalent to a sphere, a connected sum of tori, or a connected sum of projective planes.

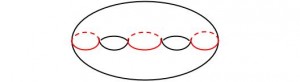
It turns out that we can cut up just about any orientable closed surface into pairs of pants with simple closed curves. This is called a pants decomposition of a surface. Pants decompositions are not unique. For example, we can cut up a genus 2 surface (a sphere with two handles) in two different ways:

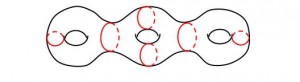
What happens in general?  Suppose our surface has \(g\) handles, where \(g\geq 2\). Then we can slice the surface with \( 3g-3\) “vertical” simple closed curves, which decomposes the surface into \(2g-2\) pairs of pants. The genus 3 case is shown below and illustrates the general idea.

Since a pair-of-pants is a subset of a thrice punctured sphere, it also admits a hyperbolic structure. Alternatively, simply construct a hyperbolic pair-of-pants by gluing together two right angled hexagons (hyperbolic) along alternate edges. More generally, it is relatively straightforward to show that there exists a unique hyperbolic pair of pants with cuff lengths \((l_1,l_2,l_3)\) , for any  \(l_1,l_2,l_3>0\). Here, cuff lengths refers to the lengths of the three boundary components. Even more can be said about hyperbolic surfaces and pants decompositions, but this will lead us too far astray.