Parametrizing Petal Projections

Posted on by

Written by Keally Rohrbacher and Sawyer Dunn-Matrullo (students in Math 383D Knot Theory Spring 2023).

Image showing a petal projection of the trefoil knot.

Figure 1: Trefoil knot petal projection.

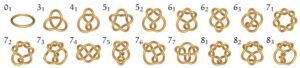
Our plan was to create models of knots with petal projections. This is a particular type of diagram of knots that has only one crossing, and a certain odd number of arcs which cross each other there. For example, Figure 1 shows the petal projection of the Trefoil Knot (image from Wikipedia). The numbers written on the arcs in Figure 1 are important, as the order in which the knot crosses through itself is what distinguishes different petal projections of knots from each other.

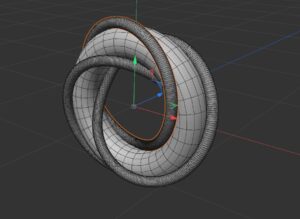
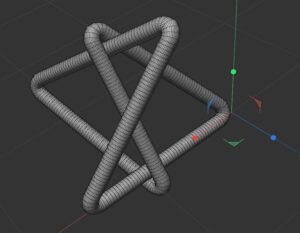
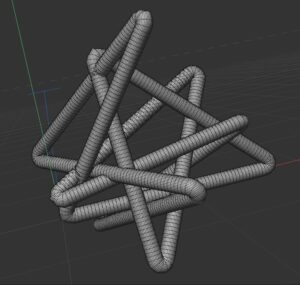
We wanted to produce 3D models of the 41, 52, and 61 knots, all of which have petal projections (shown in the figures below).

ide view of the petal projection of the 4_1 knot.

Figure 2: Side view of the petal projection of the 4_1 knot.

Since it is not important what the actual picture of the petal projection is, just that it crosses through the center in a particular order, we had some choice as to how we were doing to construct these knots. We decided that it would be interesting to construct these as parameterized functions. We knew that we could make the x and y-components of this function fairly easily using a rose curve, a type of polar function which produces a cool rose that looks just like the petal projection in 2D. So, we knew that all we had to do was come up with a function for the z-axis which would parametrize the rose curve to go around and hit the center at certain heights to produce the petal we wanted. We knew which order the strand should go through the crossing in for each knot from the paper “Knot Projections with a Single Multi-Cossing” by Colin Adams and his coauthors.

Top view of the petal projection of the 4_1 knot.

Figure 3: Top view of the petal projection of the 4_1 knot.

We considered a couple ideas for finding a function that would hit these particular heights, but ultimately decided to try to find a polynomial function.

Side view of the petal projection of the 5_2 knot.

Figure 4: Side view of the petal projection of the 5_2 knot.

We did this by creating points with the heights we needed to hit at even intervals and plugged these points into an online calculator which uses Lagrangian interpolation to produce a polynomial which hit all of these points. Once we defined this as the z-component for our function, and used the rose curve for the x- and y-components, we plugged our curve into a 3D graphing calculator called GeoGebra. The side views, in figures 2, 4 and 6 (above and below), depict these heights being hit in proper order in accordance with the Adams’ paper. The top views in figures 3, 5 and 7 show the petal projection shape of the rose curve projected to the xy-plane.

Top view of the petal projection of the 5_2 knot.

Figure 5: Top view of the petal projection of the 5_2 knot.

We ran into a couple issues during this project. The most annoying of which was trying to define our curve as a parametrized function in Cinema 4D.

Side view of the petal projection of the 6_1 knot.

Figure 6: Side view of the petal projection of the 6_1 knot.

Because we had to hit so many points, the function on the z-axis ended up being a degree 11 polynomial for both knots. And while we were able to produce this on GeoGebra, a powerful calculator, we could not make a satisfactory spline of our function in Cinema 4D. We spent a long time trying to fix this problem by manipulating points on the software. We were exasperated to find that we could simply download an .stl file directly from GeoGebra, where we already had constructed the knot, circumventing our entire issue. (Note that 3D printers use .stl files as their start point.) This made its own set of issues, however, as the shapes from GeoGebra were not smooth. But, for our final print of the knots, we also graphed the curves on Mathematica like we did in GeoGebra, again avoiding the issue of plotting a curve in Cinema 4D and Mathematica gave us models with much smoother curves.

Top view of the petal projection of the 6_1 knot.

Figure 7: Top view of the petal projection of the 6_1 knot.

The most challenging part of coming up with our functions though was creating and working with high order polynomials, but this mostly just involved us typing out long equations many times. We found that WolframAlpha easily came up with the required higher order polynomials for the 61 knot (which ended up being a degree 14 polynomial).

Tying Knots on the Shortest Lattice Walks

Posted on by

Written by Chadrack Bantange and JCW (students in Math 383D Knot Theory Spring 2023).

Background:

What is a minimal cubic lattice knot?

The cubic lattice.

The cubic lattice.

Let’s start with: what is the cubic lattice? The cubic lattice is all the points (a, b, c) in R3 such that a, b, c are integers. That is, the cubic lattice is composed of all the points in three dimensions that have integer entries. The image to the right is a depiction of the cubic lattice (from Wolfram MathWorld).

Next, what would it mean for a knot to be in the cubic lattice? Cubic lattice knots are knots whose vertices lie in the cubic lattice. That is, the vertices of the knot can be represented by (a, b, c) where a, b, c are integers.

Another way to think about cubic lattice knots would be to imagine you start your knot on the point (0, 0, 0). To take a step tracing the knot one must take one of the steps as depicted below. Observe that on this first step from the origin one has six options. One could go: left, right, up, down, forward, or back. Consider the diagram below which presents all six of the options. The step which traces the knot is itself not a part of the cubic lattice. If we move up from the origin to point (0, 0, 1) all the points between these vertices makeup the knot, but are not part of the cubic lattice per se.

Figure showing the 6 points in the cubic lattice one unit from the origin.

Figure showing the 6 points in the cubic lattice one unit from the origin.

In each of the subsequent steps you have similar options. Because you are walking within the cubic lattice, on each step you can only ever add +1 or -1 to just one of your x, y, or z coordinates to get your next vertex. Note: since we are drawing a knot, you will have one less option than when starting at the origin, because you do not want to walk back on the knot you have already drawn. If you go up from (0, 0, 0) to (0, 0, 1), then you could not go back down to (0, 0, 0) when tracing your knot.

Lastly, what is a minimal cubic lattice knot? Each knot has multiple equivalent representations and diagrams that can be reached via planar isotopies and Reidemeister moves. This means there are many versions of each kind of knot in the cubic lattice.

Consider the trefoil. One could trace a trefoil knot in the cubic lattice that globally looked somewhat smooth and like a common depiction, as below on the left. This, however, is not particularly mathematically interesting or remarkable. Rather, to ask the more interesting question we ask: what is the minimal cubic lattice knot? That is, for each of the knot equivalence classes what is the shortest walk we could take in the cubic lattice to trace out a knot in the equivalence class? On the right, observe the minimal cubic lattice knot for the trefoil. In the case of the trefoil (31), the minimal walk in the cubic lattice is 24 steps. (Left image from the Rolfsen Knot Table Mosaic.)

Figure showing the standard image of the trefoil knot (left), and the image of the minimal length trefoil in the cubic lattice (right).

Figure showing the standard image of the trefoil knot (left), and the image of the minimal length trefoil in the cubic lattice (right).

Construction

To build the cubic lattice knots, we used Cinema 4D. As part of this process, we referred to Andrew Rechnitzer’s website on plotting minimal cubic lattices). For all the cubic lattices, we noticed that when importing the data from Notepad into Cinema 4D, one line of the coordinates was missing, making the object look incomplete. This was a challenge we experienced in constructing our knots. Correcting this issue involved manually attaching numbers to each line of the coordinates while also inserting a row of zeros in the first line of the dataset. As we went on building more knots, we noticed that this process was time-consuming. Alternatively, we used Microsoft Excel to copy our coordinates from Notepad, pasted into Excel using the “paste special” option, and we were able to use Excel to automatically attach numbers to the individual coordinates. We then pasted these coordinates back into Notepad and saved it as a “txt” format.

Once the data was imported into Cinema 4D, we went to “view” in the left menu, selected “Frame Geometry” to get a better geometric view of the knot. The spline automatically connected all the points except the last to the first. Before connecting them, we first made sure that under Object manager, we have “Rectangle—Spline” selected; under “Attributes—Object—Type” ,  choose “bezier or linear” depending on how smooth we want the corners of the knot to look like. For some of the knots, “bezier” was the best smoother of the corners, while for others, “linear” was best. To connect the vertices, we selected “spline pen” and were able to click on the two, unconnected points to add the last edge to the spline.

At this point all we had was a spline made of 1-dimensional lines. In order to make the knot 3-dimensional for printing and visualization, we added “circle” and “sweep” to our Cinema 4D workspace. The circle would serve as the cross section for our knot and the sweep is what swept the circle cross section along the spline we created above. We then adjusted the radius of the knot, which in most cases was 0.25 cm. In order to smooth out the corners, we added a Chamfer to the knots and set its radius at 0.25 cm for the 3, 4, 5, and 6 crossing knots and 0.3 cm for the 7 crossing cubic knots.  We then scaled the object to be hand sized. There were a lot of variations in this regard depending on the knot, especially since some of the minimal cubic lattice knots occupied the space of a cube, while others occupied the space of a rectangular prism. In general, however, the scale ranged from 4 to 8 cm in all the three axes (x,y,z). We saved both .stl and .c4d files, ready to be printed in the IQ center at WLU.

Here are some screenshots of our work. In both cases, the standard image of the knot came from the Rolfsen Knot Table Mosaic.

On the left, the standard view of 5_2 knot. On the right, the minimal cubic lattice knot of 5_2.

On the left, the standard view of 5_2 knot. On the right, the minimal cubic lattice knot of 5_2.

On the left the standard view of the knot 6_1. On the right the minimal cubic lattice view of 6_1.

On the left the standard view of the knot 6_1. On the right the minimal cubic lattice knot of 6_1.

Flowering 3D Models

Posted on by

Written by Claire Gilreath. Joanne Wang, and Selihom Gobeze (students in Math 383D Knot Theory Spring 2023).

Building Petal Knots in Cinema 4D

Once we had found all of our coordinates for our petal knots, we were excited to actually build the knots in Cinema4D! Of course, this was not without its challenges. We started with 3_1. Our first step was to to import our points to a spline. Naturally, we ran into issues here because we were not aware that the points from the first row are read as the x, y, and z labels, so the data is not actually imported. We fixed this by editing our .txt file to include a row of 0s at the top. Also, one of the points was incorrect and we had to go back to WolframAlpha for a quick fix (this happened a couple of times throughout the process).

Image showing the petal version of the trefoil in Cinema 4D

This is the petal trefoil knot made in Cinema 4D.

At this point, we were not aware that we needed to connect the last point to the first point, so we skipped that step and decided to try the Spline Smooth tool to round out our polygonal edges. We found that the result was not as uniform as we had expected but we decided to keep going to see what would happen after the sweep. We made a circle and decided to set the radius at 0.25cm in order to avoid self-intersections but give the model enough structure to support itself. Then, we made the sweep and looked at our slightly wonky 3_1 knot. We realized that the ends were not connected so we used stitch and sew to fix that (this was a result of failing to connect the last two points of the spline). To the right is our final improved 3_1 knot.

Image showing the petal 5_1 knot in Cinema 4D.

This is the petal 5_1 knot made in Cinema 4D.

We moved on to the 5_1 knot and followed the same procedure. Once we had built it, Professor Denne looked at our slightly wonky 5_1, and suggested we try to use Chamfer tool instead of the Spline Smooth tool to make the model look smoother and more uniform, with less harsh edges of the petals. In doing this, we discovered that our last point vanished when we tried to Chamfer. We realized that we needed to close the spline by deleting our last point at (0,0,0) and using the Spline Pen to connect the first point to the last point to close the gap. We set the radius of the Chamfer to 3cm and compared our new 5_1 to the wonky one. We decided we liked the Chamfer version better and fixed our 3_1 the same way. This time we set the radius to 5cm, which we found looked much smoother and decided to stick with that for all knots. Our completed 5_1 knot is pictured above.

Image showing the petal 6_2 knot in Cinema 4D.

This is the petal 6_2 knot made in Cinema 4D.

We repeated this same process with 6_2, expecting everything to be a lot easier now that we had solidified our methods. However, this was not the case. As we rotated around the knot after sweeping, we noticed that we had a self-intersection at one point and two strands that were concerningly close together. Though we’re not entirely sure why this happened, we think the Chamfer forced the two strands too close together. We first tried to make the radius of the circle inside the sweep smaller, but the strands were still touching at 0.17cm, so we decided to manually pull the spline points apart after the Chamfer but before the sweep. This fixed our problem and everything looked good after the sweep this time. Our completed 6_2 knot is pictured above.

As we built 6_3 we were worried about self-intersections, since the (x,y) coordinates were the same as in 6_2. We did not run into any problems this time, perhaps because of the different heights. Below is a picture of 6_3 from four angles, showing the “nice” petal view as well as the less attractive side views.

Different views of the petal 6_3 knot made in Cinema 4D.

Different views of the petal 6_3 knot made in Cinema 4D.

 

 

Trig Trials

Posted on by

Written by Claire Gilreath. Joanne Wang, and Selihom Gobeze (students in Math 383D Knot Theory Spring 2023).

Finding the Coordinates of Petal Knots

We decided we wanted to try to 3D print the petal projections of knots for our project because they looked pretty and seemed like a challenge.

Image showing the trefoil knot in petal form.

A petal projection of the trefoil knot.

Petal projections of knots are projections where all of the crossings are aligned through a single line in 3d space, giving the knot a flower-like appearance. A two-dimensional petal projection of the trefoil (3_1) is pictured to the right (via this image from Wikipedia). We decided to work on creating petal versions of 3_1, 5_1, 6_2, and 6_3 knots. We relied heavily on the work described in Colin Adams’ “Knot Projections with a Single Multi-Crossing” paper. In the appendix of this paper, Adams and his coauthors described the order of each petal for the knots we hoped to construct. Also, we utilized the Wikipedia page  about petal projections of knots to better understand their structure.

We were a bit uncertain of the best method to create these knots, since as far as we knew, there were no equations we could plug into Cinema 4D, nor were there coordinates constructed by someone else. After talking to Professor Denne, we felt that our best bet would be creating our own sets of coordinates using trig and polar coordinates. We decided to find four points per petal: the center, the top of the arc of each petal, and the end of both edges. To do this we constructed a circle through the ends of the edges, shown in red in the diagram of the trefoil below.

This figure shows the details behind the computations needed to find the coordinates of points along the petal trefoil knot.

This figure shows the details behind the computations needed to find the coordinates of points along the petal trefoil knot.

We then found the angle between each of the edges using the formula Pi/(number of petals), so for the trefoil, we had Pi/5. The length of each red edge was the radius of the circle, r, which we determined in a later step after finding the heights. Next, we added lines from the top of each petal to the center of our circle, shown in green, and found the angle between these lines using the formula 2Pi/(the number of petals), this was 2Pi/5 for the trefoil. To find the length of the green lines, we treated the curved part of the petal as a semicircle and found its radius by finding the length of the chord between the two red edges and dividing by 2. We then found the length of the other piece by using the Pythagorean theorem and added both measurements together. These calculations are shown in purple in the diagram above, where the length of the green line is given by the following formula: the square root of (r2.-(r*sin(Pi/5))2) plus r*sin(Pi/5). Using trig, this is r(cos(Pi/5)+sin(Pi/5)). We called this quantity x as we labeled the points of the trefoil in the diagram above.

The next step was to find the heights of each point and then convert everything into Cartesian coordinates in order to have points that Cinema4D could understand.

Image of the petal trefoil knot with details of the heights of the points.

This figure shows the heights given to the points on the petal trefoil knot.

We used the orders from the last page of Adams’ paper which gave us the heights for the edges at (0,0). We also assigned heights to the points we found by averaging the heights of the edges to find the height for the top of the petal. We then averaged the height of the top of the petal and the edges at (0,0) to find the height of the end of each edge. For the trefoil, we came up with the heights to the right and then scaled them up by 1.5, so our model would be a bit larger after printing. This also guided our decision to make the radius of our circle (r) be 3 for 3_1 and 5_1. We used r = 3.5 for 6_2 and 6_3.

 At this point, we had found the polar coordinates for all of the points we wished to plot in Cinema4D, so we converted them to decimal approximations with the help of WolframAlpha. The Cartesian coordinates of 3_1 are shown in the table below. We followed a similar process for 5_1, 6_2, and 6_3 knots. Points completed!

Vertex x y z
1 0 0 6
2 -0.927050983 2.853169549 4.875
3 0 4.19040674 3.75
4 0.927050983 2.853169549 2.625
5 0 0 1.5
6 -0.927050983 -2.853169549 2.25
7 -2.463059283 -3.390110266 3
8 -2.427050983 -1.763355757 3.75
9 0 0 4.5
10 2.427050983 1.763355757 3.375
11 3.985313636 1.294906896 2.25
12 3 0 1.125
13 0 0 0
14 -3 0 0.75
15 -3.985313636 1.294906896 1.5
16 -2.427050983 1.763355757 2.25
17 0 0 3
18 2.427050983 -1.763355757 3.75
19 2.463059283 -3.390110266 4.5
20 0.927050983 -2.853169549 5.25
21 0 0 6

 

The Figure-8 Knot and its Mirror Image

Posted on by

Written by Elizabeth Marshall, Mason Shelley, and Libby Kerr (students in Math 383D Knot Theory Spring 2023).

We built different models depicting how the figure-8 knot 41 is achiral, meaning the knot is equivalent to its mirror image. In this case, if we were given a knot diagram, its mirror image would be the same diagram with swapped crossings. We observe some knot theory facts: the figure-8 knot (41) is a 1 component alternating knot with a crossing number of 4 and an unknotting number of 1. The crossing number of a link is the minimum number of crossings needed in a diagram, and the unknotting number is the minimum number of times the knot must pass through itself before it becomes the unknot. While the knot looks trivial, its composition is surprisingly difficult to model.

Starting with a mirror image of the figure-8 knot (Step 1 below), each of the subsequent steps shows one or two R-moves that lead the knot back to its original state. An R-move is a simple manipulation of a piece of the knot in space, where a series of them can result in significant alteration of the knot. The steps are as follows:

Step 1: Start with a Figure-8 knot with opposite crossings.

Step 1: Start with a Figure-8 knot with opposite crossings.

Step2: Make an R-2 move that forms two “over” crossings on top of the figure-8 shape of the knot.

Step2: Make an R-2 move that forms two “over” crossings on top of the figure-8 shape of the knot.

Step 3: Make an R-3 move that brings the arc on the left of the figure-8 shape to the center of the diagram.

Step 3: Make an R-3 move that brings the arc on the left of the figure-8 shape to the center of the diagram.

Step 4: Make an R-2 move that pulls the now central arc over to the right of the main shape.

Step 4: Make an R-2 move that pulls the now central arc over to the right of the main shape.

Step 5: Complete an R-3 and an R-1 move that form an outer arc to the top right.

Step 5: Complete an R-3 and an R-1 move that form an outer arc to the top right.

Step 6: Finally, make an R-1 move that results in the figure-8 knot.

Step 6: Finally, make an R-1 move that results in the figure-8 knot.

Step 7: Flip the figure in Step 6 180 degrees. This move reveals the Figure 8 knot with crossings that are the opposite of those seen in Figure 1.

Step 7: Flip the figure in Step 6 180 degrees. This move reveals the figure-8 knot with crossings that are the opposite of those seen in Figure 1.

We used Cinema 4D to develop our models. On this software, we used the drawing tool to build our original knot shown in Step 1. To draw the subsequent steps representative of the R-moves we manipulated the knot from the previous step, scaled it appropriately, and checked to make sure all crossings were correct.

Using new software presented numerous challenges that we faced throughout the project. We initially found parametric equations on Wikipedia for the figure-8 knot that resulted in the wrong knot when visualized in Mathematica and then resulted in a simple line in space when entered in Cinema 4D. This meant that the this parameterization was not going to work. Without these equations, we were forced to draw the knot using the spline pen. It took nearly 10 attempts to draw the first image of the knot but eventually, we made a cohesive, recognizable figure-8 knot.

Using this tool, created one big challenge with regards to placing the points for future manipulation during the design process. Our most successful strategy was to draw the structure of the knot in 2D (holding the z-axis flat) and manipulating the points to create the over/under crossings after the knot was drawn.

Another challenge was figuring out how to properly demonstrate the transition of the knot’s mirror image back to its original state. In order to make the manipulations clear, we made a video showing the use of R-moves to visualize how the diagrams were interconnected.

Towards the end of our design process, we decided to take out the 6th step (shown above) because there was too much similarity between steps 6 and 7 (final model); that is why you’ll see 7 steps and only 6 models.

Overall, the main challenge that we ran into was using the software and properly putting our ideas into the diagrams. A massive help to our group was Dave Pfaff (IQ Center WLU), who is the expert that helped us navigate Cinema 4D. Thank you so much Dave, all of your help is greatly appreciated.

New Torus Link, Improved Visualizations, and Cinema 4D Problems.

Posted on by

Written by Hillis Burns, Shannon Timoney, Hall Pritchard (students in Math 383D Knot Theory Spring 2023).

We created the T(2, 8) torus link (or 821 link) using Cinema 4D. The equations for this two component link are x = Cos[t]*(3+Cos[4t]), y = Sin[t]*(3+Cos[4t]), and z = Sin[4t]. The second component is created by the equations x = Cos[t]*(3+Cos[4t+Pi]), y = Sin[t]*(3+Cos[4t+Pi]), and z = Sin[4t+Pi].

We also created the T(3, 3) torus link (or 632 link). With the  632 link, each of the three components goes around the longitude once and goes around the meridian once. The equations for this knot are x1 = Cos[t]*(3+Cos[t]), y1 = Sin[t]*(3+Cos[t]), z1 = Sin[t], x2 = Cos[t]*(3+Cos[t+2*Pi/3]), y2 = Sin[t]*(3+Cos[t+2*Pi/3]), z2 = Sin[t+2*Pi/3], and x3 = Cos[t]*(3+Cos[t+4*Pi/3]), y3 = Sin[t]*(3+Cos[t+4*Pi/3]), z3 = Sin[t+4*Pi/3].

Image showing the T(3,3) torus link lying on the torus.

The T(3,3) torus link shown lying on the torus.

After creating the T(3, 3) or 632 link, we wanted to build a model that helps demonstrate what the torus link actually is. We did this by first opening back up the T(3, 6) or 632  in Cinema 4D. Then we created a torus surface and rotated it 90° so that the torus link sat in the right position on the torus surface. Then we changed the radius of both the meridian and the longitude so that the 3d model was in a presentable format. Our final model which is shown above gives a good physical representation of how a torus link is constructed.

We also created the  T(3, 6) torus link (or 633 link). With the 633 link, each of the three components goes once around the longitude and goes three times around the meridian. The equations for this knot are x1 = Cos[t]*(3+Cos[2t]), y1 = Sin[1t]*(3+Cos[2t]), z1 = Sin[2t], x2 = Cos[t]*(3+Cos[2t+2*Pi/3]), y2 = Sin[t]*(3+Cos[2t+Pi]), z2 = Sin[2t+2*Pi/3], and x3 = Cos[t]*(3+Cos[2t+4*Pi/3]), y3 = Sin[t]*(3+Cos[2t+4*Pi/3]), z3 = Sin[2t+4*Pi/3].

While using the Cinema 4D software, the biggest problem we had was fixing the join at the end of two strands. In Cinema 4D, the join will sometimes not look correct. In order to fix this, we will first decrease the period of the parametric equations in order to make the join fully noticeable. We decreased it from 2π (~6.28) to 6.275.

Image showing the two ends of the torus link with too many points highlighted

Too many points are highlighted near the ends of the torus link.

We then try to highlight all the points at the end of the knot, in order to use the “stitch and sew” function. We came across problems when we accidentally highlighted other points not at the end. This is shown in the figure to the right. This would happen more often when we increased the sample size to a number that was higher than necessary (>300). This is the case in the image below. By decreasing the sample size, it made it easier to highlight just the end points of the knot, as shown below. At this point we were able to successfully use the “stitch and sew” function.

Image showing points highlighted along the ends of the torus link.

This image shows that just the end points of the two ends of the torus link are highlighted. This allowed us to successfully use the Stitch and Sew function to join the ends together.

Overview of Torus Shapes, Knots, and Links

Posted on by

Written by Hillis Burns, Shannon Timoney, Hall Pritchard (students in Math 383D Knot Theory Spring 2023).

Image of a torus with a 3 component link on it

The T(3,6) torus link.

The torus is the surface of a donut in 3-dimensions. A torus knot/link is a knot/link that can be moved to lay on the torus surface in R3.The image on the right shows a link being wrapped to lie on a torus; this is the T(3, 6) or 633 torus link. Knots are also commonly described in knot tables using the notation, Crnj. The crossing number is denoted by Cr, the number of components by n, and the certain configuration is j. As seen in this image, the torus has two key circles: the longitude, which wraps around the long way of the torus, and the meridian, which wraps around the short way. These are illustrated in the image below.

Image of a torus showing the longitude and meridian curves

A torus with some Longitude and Meridian curves highlighted.

The notation for torus knots is T(p, q); The knot wraps around the longitude p times, while it wraps q times around the meridian. The two figures are from a Mathematica file which visualizes torus links, and this website. This Knot Plot website also has a neat table showing many of the torus knots and links.

Using a Mathematica file provided by Professor Denne, we were able to start creating the T(2, 4) torus link (or 421) in Cinema 4D. This is a two-component link where each component goes once around the longitude and twice around the meridian, as illustrated below.

Image showing the T(2,4) torus link

The T(2,4) torus link.

The parametric equations that create the link are x =  Cos[t]*(2+Cos[2t]), y = Sin[t]*(2+Cos[2t]), z = Sin[2t], with t going from 0 to 2Pi. However, for this link there are two components. Thus, a second equation was needed for the second component. To create a torus link like this, the second equation must be rotated 180 degrees to fit with the first curve. To do that, we added Pi to the trigonometric equations of the first sweep: x = Cos[t]*(3+Cos[2t+Pi]),  y = Sin[t]*(3+Cos[2t+Pi]), z = Sin[2t+Pi].

We also decided to create the T(2, 11) torus knot (also known as 111) in addition to the links in Cinema 4D. This is a knot (one component link) where the curve goes twice around the longitude and 11 times around the meridian. The topmost figure below shows the original image of the torus knot that we created. The knot does not look smooth, as Cinema 4D only evaluated a few points along the parametrized curve. However, after adding more sample points we were able to make the torus knot smoother. The progression of sample points, from 20, to 50, to 100, to 200, is shown from top to bottom:

T(2,11) with 20 sample pointsT(2,11) with 50 sample points

T(2,11) with 100 sample pointsT(2,11) with 200 sample pointsWe also had to adjust the radius because the loops were too close together. In order to spread out the components, the radius was changed from 2 to 3.

Next, we created a T(2, 6) torus link (or 621) in Cinema 4D. With the 621, each of the two components goes once around the longitude and three times around the meridian. Using the Mathematica file, we knew that the equations for this link were, x = Cos[t]*(3+Cos[3t]),  y = Sin[t]*(3+Cos[3t]),  z = Sin[3t].  The second component’s equations, again rotated by Pi, consist of, x = Cos[t]*(3+Cos[3t+Pi]), y = Sin[t]*(3+Cos[3t+Pi]),  z = Sin[3t+Pi].

3D Printed 7_1 Mosaic Knot

Posted on by

Written by Sion Jang and Charlotte Peete (students in Math 383D Knot Theory Spring 2023).

The mosaic number for the 71 knot is six, meaning that it cannot be created on a grid using mosaic tiles smaller than 6 x 6. We are creating a 3D version of 71 mosaic knot using Cinema 4D as our main design program. We created this knot using the same method as our Trefoil knot. However, we made changes to the Chamfering process, the diameter of the tube, and the distance between some of the over-strands and feet.

When creating this knot with the same process as the Trefoil and Figure-8 knots, we came across a few problems.

The arrows show the three feet where the z-coordinates were changed.

Figure 1: The red arrows show the three feet where the z-coordinates were changed.

Since the 71 knot has more crossings than either of the other two knots we created, we found that the close proximity of the feet would lead to self-intersections. We first changed the diameter of the circle from 6 to 4 mm. While this change helped to solve the intersection problem, the feet still seemed to be close together. Aesthetically, we still weren’t satisfied with how crowded the feet looked. So, we changed the z-coordinates of the horizontal feet to create more space between the adjacent vertical feet. The arrows in Figure 1 point to the three feet for which we changed these coordinates. Figure 2 shows an overhead view of the spacing between the feet with these changes.

Overhead view shows spacing between alternating feet.

Figure 2: Overhead view shows spacing between alternating feet.

The biggest challenge we came across with this knot was figuring out how to properly curve vertices without distorting the rest of the knot. Our original method of Chamfering did not work because there wasn’t enough space between the curves of the knot and the feet. To fix this problem, we added an additional point next to each vertex of the over-strand immediately before the foot. These points were added as close to the original vertices as possible.

Figure 3 shows our final product.

Finished 7_1 mosaic knot.

Figure 3: Finished 7_1 mosaic knot.

 

3D Printed Trefoil Mosaic Knot

Posted on by

Written by Sion Jang and Charlotte Peete (students in Math 383D Knot Theory Spring 2023).

Mosaic knot theory uses a combination of the following eleven tiles to create a knot or a link representation on an nxn grid. These tiles are shown in Figure 1.  As explained in the Knot Mosaic Tabulation paper by Hwa Jeong Lee, Lewis D. Ludwig, Joseph S. Paat, and Amanda Peiffer, the mosaic number of a knot K is the smallest integer n for which K can be represented on an  mosaic board. This mosaic number is a knot invariant and can be used to distinguish between two knots.

Tiles used to create mosaic knots

Figure 1: tiles used to create a mosaic knot or link.

The Knot Mosaic Tabulation Paper provided the minimal grid mosaic diagrams for all 36 prime knots of eight crossings or fewer. The mosaic number for a trefoil is four, m(31)=4. Thus, a trefoil cannot be created on a 3 × 3 grid, and the minimum grid needed is a 4×4 grid. We created a 3D version of 31 Trefoil mosaic knot using Cinema 4D as our main design program. To create this knot, we first drew a coordinate plane onto the diagram of the Trefoil knot, as shown in Figure 2.

Mosaic trefoil knot with coordinates in xy-plane

Figure 2: Trefoil mosaic knot with coordinates in xy-plane.

We did this so that we could insert integer coordinates into Cinema 4D that would allow for accurate spacing in our knot. Our final knot was scaled to be around 7×7 cm without the circle sweep, which is the thick tube around the curve.

One of the main challenges we encountered in constructing this knot was figuring out how to represent the over and under-crossings. Using this blog by Laura Taalman as inspiration, we decided to create “feet” for our knot. The distance from the center of each foot to the center of the over-strand is 1 cm. We also put a .125 mm space on either side of the over-strand between the legs to show that the strands are not connected. Figure 3 shows a close-up representation of one of the feet and legs on this knot.

Close-up image of the legs and feet of an under-strand.

Figure 3: The foot and two legs create a strand which crosses under a different strand of the knot.

The coordinates we chose made the knot have an angular rather than curved shape, and we manually curved the knot in Cinema 4D using the “Chamfer tool” once our knot was constructed. Figure 4 shows our knot before we curved the edges. Figure 5 shows our knot after we curved the edges. For the different curves, we used different values of the Chamfer to get the desired look.

Top view & angled view of the trefoil knot showing the sharp corners.

Figure 4: Top view & angled view of the trefoil knot before curving the corners.

Top view & angled view of the trefoil knot after curving the corners.

Figure 5: Top view & angled view of the trefoil knot after curving the corners.

The Figure-8 mosaic knot

FIgure 6: The figure-8 mosaic knot.

Using this same process, we created 41, the Figure-8 knot. The final product is shown in Figure 6.

Modeling and 3D-Printing Equilateral Stick Knots

Posted on by

Written by Aidan Aengus Kitchen, Arun Ghosh, and Alex Wolff (students in Math 383D Knot Theory Spring 2023).

Brief Math Background:

Image showing knots with 3, 4, 5, 6, 7 crossings, and a few 8 crossing knots.

Knot table. Image from https://knotplot.com/zoo/

A knot is a simple, closed curve in space. This means that it forms a closed loop and does not intersect itself. The figure to the left illustrates the simplest knots with 0 to 8 crossings (from https://knotplot.com/zoo/).  The knots are labelled with the crossing number and a subscript which is a number that distinguishes between different knots with the same number of crossings. A polygonal knot is composed of a finite number of edges or straight sticks. For an equilateral stick knot, the edges have the same length.  We constructed equilateral stick knots representing the knots shown above. In the models we made, we used the minimum number of sticks necessary to construct the knots.

Clayton Shonkwiler is an Associate Professor of Mathematics from the University of Colorado. His primary research is using geometry to solve topological and physical problems. His recent work published in 2022, New Stick number bounds from random sampling confined polygons, looks at equilateral stick knots. The paper focuses on finding the upper and lower bounds for stick number and also gives the coordinates for constructing the knots in 3 dimensional space. These coordinates can be found in following GitHub repository: https://github.com/thomaseddy/stick-knot-gen/tree/master/stick_number/mseq_knots

The table below displays the crossing number of the knots we constructed, as well as the number of sticks we used for each one.

Knot Crossing # # of sticks used
31 3 6
41 4 7
51 5 8
52 5 8
61 6 8
62 6 8
63 6 8
71 7 9
72 7 9
73 7 9
74 7 9
75 7 9
76 7 9
77 7 9
949 9 9
K11a1 11 12
K12n63 12 11

How We Built the Knots:

For each knot, we first retrieved the coordinate data from the GitHub repository and saved it in a text file. Then, we imported the data into Cinema4D by creating a linear spline object, opening the Structure window, clicking on “Import ASCII Data” and navigating to the text file. In order to close the knot, we had to add a point at the origin and connect it to the last point in the imported data using the Spline Pen.

Image showing the 3_1 equilateral Stick Knot.

3_1 Equilateral Stick Knot.

Then, we resized the spline to 6-7 cm for each dimension, and swept a circle of radius 0.3 cm around the spline, creating a tube around the knot. We did this to make the knots 3-dimensional, because we cannot 3D-print a spline (a 1-dimensional object in 3D space). To round the corners, we used the Chamfer function. Finally, we exported the models as .stl files and 3D printed them. In total, we designed all of the equilateral stick knots with three, four, five, six, and seven crossings. Additionally, we modeled knots with higher crossing number, such as 949, k11A1, and k12N603. The images above and below depict the 31 and 61 equilateral stick knot models.

An image of the 6_1 equilateral stick knot

6_1 Equilateral Stick Knot

Challenges and Observations:

  • Scaling
  • Self-intersections
Image showing self-intersections in the 6_1 knot

Self-intersections in the 6_1 knot

Initially, we did not scale our models to the appropriate size (suggested 6-7cm, or palm size). We also moved vertices around in the original 63 model, so the sticks lengths were altered, and we had to redo it. Additionally, the radius of the sticks was too small to neatly 3D print a label on the physical knot, so we decided to tape the labels on after the knots were printed. One interesting observation we made was increasing the radius of the tubes created self-intersections between the “tubes” that were not evident in the spline. The images above and below highlight self-intersections in the 61 and K12n630 models.

Image showing self-intersections in the K12n630 knot

Self-intersections in the K12n360 knot.