At the end of April I headed down to Athens Georgia to visit my friend and collaborator Professor Jason Cantarella at the University of Georgia, Athens. While there I had the opportunity to visit the Double Helix STEAM school and talk with the students about Different kinds of geometry, in particular hyperbolic planes.

We started by discussing planes, spheres and the hyperbolic crocheted planes I bought. We talked about triangles and the interior angle sums of the different triangles (\(180^\circ, \, >180^\circ,\,  <180^\circ\) respectively). The students found the idea of great circles and spherical triangles pretty mind blowing, especially when I gave them an example of a triangle with three \(90^\circ\) angles. However, they were quickly on board and immediately suggested spherical triangles with even larger internal angle sums.

We then talked about the way a plane can be tiled with hexagons, and then how a soccer ball is made by switching out a hexagon (6-gon) with a pentagon (5-gon).  Since there is less material, the surface has the positive curvature of a sphere. A model of a hyperbolic plane can be made when a hexagon is replaced with a heptagon (7-gon).  The extra material gives the negative curvature of the hyperbolic plane. 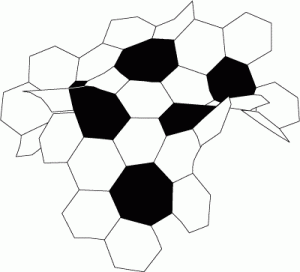The Institute for Figuring has some great information about this model and has instructions for building one too. We used these instructions to build our own hyperbolic planes.  The students used scissors and sticky tape to construct their models. They were awesome!